VOYAGER 2
FIND OUR PRESENTATION VIDEO HERE:
Part A : About Voyager 2
| Voyager 2 |
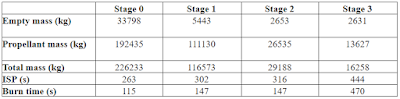
Voyager 2 was launched at the Space Launch Complex 41, Cape Canaveral, Florida on August 20th, 1977 at 14:29:00 UTC. The rocket it used was Titan IIIE, which has 4 stages and a load capacity of 15400 kg.
One of the missions of Voyager 2 is to observe four largest and outermost planets on our solar system which are Jupiter, Saturn, Uranus and Neptune. Through calculations, trajectories for its flight can be done once every 156 years. Starting with its launch on 20 August 1977, then entering the Jovian System (the Jupiter observation stage) on 8 July 1979 with its closest distance being 721670 km from Jupiter's center of mass. Furthermore, it enters the Saturnian system (the Saturn observation stage) on 22 August 1981 with its closest distance being 161000 km from Saturn's center of mass. Following this, it entered the Uranian system (the Uranus observation stage) on 24 January 1986 with its closest distance being 107000 km from Uranus' center of mass. Lastly, the Neptunian system (the Neptune observation stage) on 25 August 1989 with its closest distance 4950 km. Afterwards, Voyager 2 enters the interstellar mission stage.
References:
https://voyager.jpl.nasa.gov/mission/timeline/#event-a-once-in-a-lifetime-alignment
https://en.wikipedia.org/wiki/Voyager_2#Launch_and_trajectory
http://www.astronautix.com/t/titaniiie.html
Part B : Reconstruction of Trajectory
1. Heliocentric Trajectory
We used the Hohmann approach in Interplanetary Trajectory of the Voyager 2. With this approach, it is assumed that the orbit plane is parallel and thus the two body problem analysis can be done.
Thus, the time required for the Hohmann transfer orbit from Earth to Jupiter is as followed:
2. Hyperbolic Escape Trajectory
Orbital transfer from the parked orbit (Earth's orbit) to the hyperbolic escape trajectory
To conduct an analysis on the hyperbolic escape trajectory, assumptions are made namely:
- Location of the rocket's launch is on the Earth's pericenter (Earth is on apohelium).
- Other sky objects are ignored to acquire a two body problem.
- Rocket, Earth, Jupiter and Sun's orbits are on the same plane to acquire a one plane analysis.
- Impulsive thruster
- Course correction is neglected.
Firstly, the velocity of the rocket during parked orbit is calculated
Afterwards, the velocity of Earth relative to the Sun is calculated
The velocity of rocket in apohelium is
After the above are calculated, thus we can acquire the escape velocity of the rocket from the Earth satellite which is
Vw,apohelium= V∞ + VE,S
V∞ = Vw,apohelium – VE,S = 6.97 km/s
The characteristic energy of the hyperbolic trajectory (C3) can be calculated as followed
C3 = V∞2 = 48.54 km2/s2
Thus, the hyperbolic parameter of the rocket on Earth's orbit is
The hyperbolic pericenter velocity of the rocket on Earth's orbit is
Thus, the change in velocity for the rocket to escape the Earth is
The mass of the propellant needed during this stage is:
where in:
M0 = 632970 kg
g0 = 9,8 x10-3 km/s2
Isp = 444 s
3. Hyperbolic Arrival Trajectory
Orbital transfer from the hyperbolic escape trajectory to Jupiter's orbit
To conduct an analysis on the hyperbolic arrival trajectory, assumptions are made namely:
- Rocket arrives on the pericenter of Jupiter and Jupiter is on the perihelium.
- Other sky objects are ignored to acquire a two body problem.
- Rocket, Earth, Jupiter and Sun's orbits are on the same plane to acquire a one plane analysis.
- Impulsive thruster
- Course correction is neglected.
Then, the rocket velocity when it is Jupiter's orbit is calculated, with the known altitude of 570000 km, thus the parameter of orbit is:
Then, the velocity of Jupiter is calculated relative to the Sun:
Then, the velocity of the rocket in perihelium is calculated:
Thus, we can acquire the escape velocity from Earth's satellite:
The velocity of the hyperbolic pericenter in Jupiter's orbit would be:
The change in velocity required to escape from Earth is:
The propellant mass required is:
where in:
M0 = 825.5 kg
g0 = 9,8 x 10-3 km/s2
Isp = 205 s
Comparison table between calculation and reference results
There is a difference in the reference and calculated values. This could occur due to the assumption done during the calculation. We are assuming that the planes are one, although in reality, there is an inclination during the orbital transfer towards Jupiter. We did not do the course correction as well. The error in the mass of propellant needed in the parked orbit (Earth's orbit) to the hyperbolic escape trajectory is relatively small because course correction has not been done. Meanwhile the mass of propellant needed in the hyperbolic escape trajectory to Jupiter's orbit has a large error due to the fact that we did not review the course correction twice.
Part C : Data used in calculation
RE: 149600000 km
RJupiter: 778500000 km
rJupiter: 69111 km
rE: 6371 km
µE = 3,986 x 105 km3/s2 (Earth gravitational parameter)
µSun = 1,327 x 1011 km3/s2 (Sun gravitational parameter)
µJupiter = 1.266 x 108 km3/s2 (Jupiter gravitational parameter)


Comments
Post a Comment